Exercise 4-26(2)
Choose a nontrivial Cost-category \(\mathcal{X}\) and draw a bridge-style diagram of the unit profunctor \(\mathcal{X} \overset{U_\mathcal{X}}\nrightarrow \mathcal{X}\)
Solution(1)
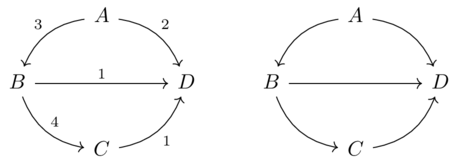
becomes
Because Feas is a category, we can describe feasibility relation using one-dimensional wiring diagrams:
\(\xrightarrow{a}\boxed{f}\xrightarrow{b}\boxed{g}\xrightarrow{c}\boxed{h}\xrightarrow{d}\)
We need more structure to talk about multi-input/output case.
This chapter restricts discussion to skeletal quantales, but it is not hard to extend to non-skeltal ones. Two ways:
Let morphisms of \(\mathbf{Prof}_\mathcal{V}\) be isomorphism classes of \(\mathcal{V}\) profunctors. (analogous to trick used when defining Cospan category.)
We could relax what we mean by category (requiring composition to be unital/associative ‘up to isomorphism’ ... this is known as bicategory theory).
The category \(\mathbf{Prof}_\mathcal{V}\), given a skeletal quantale \(\mathcal{V}\)
Objects: \(\mathcal{V}\) categories
Morphisms: \(\mathcal{V}\) profunctors, composed according to Definition 4.21
Identities are unit profunctors
The category Feas
Instantiate a \(\mathbf{Prof}_\mathcal{V}\) category with \(\mathcal{V}=\mathbf{Bool}\)
Due to skeletality, we need to show for all inputs that \(\phi \leq U_P;\phi\) and \(U_P;\phi \leq \phi\) (the second equality to show is done similarly).
Forward direction
\(\phi(p,q) = I \otimes \phi(p,q)\)
due to unitality of \(I\) in a symmetric monoidal preorder.
\(\leq P(p,p) \otimes \phi(p,q)\)
This is because \(\forall p \in P:\) \(I \leq P(p,p)\) (a constraint of a \(\mathcal{V}\) category), the reflexivity of \(\leq\) for \(\phi(p,q)\), and the monotonicity of \(\otimes\).
\(\leq \underset{p' \in P}\bigvee(P(p,p') \otimes \phi(p',q))\)
The join is a least upper bound, and the LHS is an element of the set being joined over (the case where \(p=p'\)).
\(= (U_P;\phi)(p,q)\)
This is the profunctor composition formula, subtituting in the unit profunctor definition explicitly.
Reverse direction
Need to show \(\underset{p' \in P}\bigvee(P(p,p')\otimes \phi(p',q)) \leq \phi(p,q)\)
Show that this property holds for each \(p' \in P\) - given the join is a least upper bound, it will also be less than or equal to \(\phi(p,q)\)
\(P(p,p')\otimes\phi(p',q) = P(p,p')\otimes\phi(p',q)\otimes I\)
due to unitality of \(I\) in a symmetric monoidal preorder.
\(\leq P(p,p')\otimes \phi(p',q)\otimes Q(q,q)\)
\(\forall p:\) \(I \leq P(p,p)\) (a constraint of a \(\mathcal{V}\) category) and the monotonicity of \(\otimes\).
\(\leq\phi(p,q)\)
This was shown in Exercise 4.9
The unit profunctor is unital, i.e. for any profunctor \(P \overset{\phi}\nrightarrow Q\): \(U_P;\phi = \phi = \phi; U_Q\)
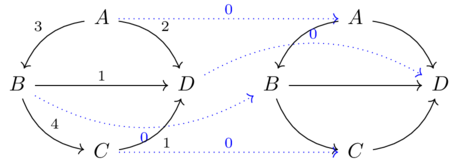
Choose a nontrivial Cost-category \(\mathcal{X}\) and draw a bridge-style diagram of the unit profunctor \(\mathcal{X} \overset{U_\mathcal{X}}\nrightarrow \mathcal{X}\)

becomes

Justify all steps the proof of the unitality of unit profunctors.
In the case of \(\mathcal{V}=\mathbf{Bool}\) show each step in the forward direction is actually an equality. NOCARD
Done, see the proof
\(\forall p: P(p,p)=true\) for a Bool-enriched category, because that is the only option for \(I=true\leq P(p,p)\)
\(true \land x = x\)
If \(\phi(p,q)\):
then at least one element of the set being joined over is true (where \(p=p'\) such that \(P(p,p')\land \phi(p',q) = true\)), and the least upper bound of such a set is \(true\)
Else:
Then every element of that set is \(false\) such that the join is also \(false\).
If \(p\leq p'\), it fails because of the second conjunct (consider the constraint on profunctors: we are demanding equal or more resources than something we know fails)
If \(p \not \leq p'\), it fails because of the first conjunct. In a Bool-category \(P\), \(P(a,b)\) iff \(a \leq b\).
Prove that the serial composition of profunctors, \(\mathcal{X}\overset{\phi}\nrightarrow\mathcal{Y}\) and \(\mathcal{Y}\overset{\psi}\nrightarrow\mathcal{Z}\), is associative.
This is tantamount to the quantale matrix multiplication being associative, which was shown in Exercise 2.104.